The further I go in teaching the more value I see in looking back at mathematical journeys that students take through primary school, including very early on. The common misconceptions at primary level go some way to explain why students have problems that they encounter later on, when challenged in different ways.
An example of this is with negative numbers. A standard approach I took to student difficulties with negative numbers through the first part of my teaching career was to draw a vertical number line and talk about jumps on that vertical number line. It was only after listening to Bernie Westacott on a Craig Barton podcast, that I realised that the concept of integers as points on a number line is something that causes great difficulties in primary school and is something that students really have to work on. With that in mind, I was far more successful in approaches to negative numbers when I looked at a number track, or with double sided counters, which give the integers as discrete units. Once we’d established that we could take that next step up. This was a really important lesson for me in meeting students where they are at and then taking them with you.
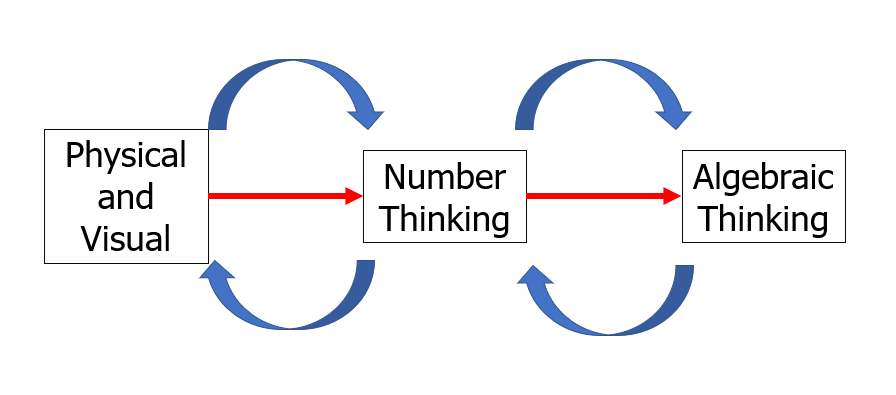
The above diagram is the prism through which I see mathematical understanding currently. We move slowly from left to right, and we make jumps as we specialise or generalise where required.
I teach and have always taught in a school which is a 14-19 school (not for much longer!). Therefore, with students starting in Year 10, I think I have been guilty, often, and especially early in my career, of completely ignoring the left hand side of this diagram. If we ignore the left hand side of the diagram we risk giving students a lack of depth of understanding, or lack of appreciation for the connectivity of maths, an inability to specialise if they are stuck, a sense that number/algebra has greater value. Where we start when we teach a new topic is vital in terms of meeting students where they are at and taking them with you.
The Open Box
I don’t want to focus on the physical/visual in this piece, as many have written about this, including myself (in particular about surds), but the connection between number and algebra is often seen as a one way street with algebra very prominently being the generalisation of number and seeing the effects of algebra in number allows us to scaffold the algebra on. However, what I aim to show in this piece is that we can use a technique to show the two worlds alongside each other in multiple topics.

In an open box we can put numbers.
An open box is a window between number and algebra.
Different algebraic forms could see the open box as either hiding a missing figure, or an open vessel for different numbers.
An open box is unthreatening. An open box is inviting. Students bring with them an understanding of what an open box can mean, in the way that x does not (until we have built that comfort in the world of algebraic understanding)
Questions like this from multiple primary worksheets that I found on the internet show that window in action early on. I’ve even seen an open box used on Numberblocks!

Here the window hides a specific answer, but with very simple changes we could make it an open vessel able to carry some or all numbers, or to generate relationships between numbers.
Consider the difference between the previous example and these:

At the moment there are no rules here, but trying to place constraints on these leads to potentially rich mathematical discussion – if you limit to the same number having to go in each box, how come the middle one has ALL solutions, but the final one has NO solutions? An open box also encourages creativity – who can impress me with what they have put in?
The box could easily be replaced by an algebraic term. However, this is our scaffold between the numerical use and the algebraic use. The box acts as the window between the two worlds, and allows us to see both concurrently, or to aid us to view from one world a perspective of the other.
Early maths understand the use of the box in the context of early algebraic thought, but the threads that tie this together become frayed as we move on later through KS3 and KS4. In the remainder of this blog post I want to view how the open box allows us to further understanding at the secondary level.
Equations
At a mathsconf in June 2019 I was in a workshop where we were encouraged to work together and I had a big old barney with the rest of the table about solving equations like this:

The prevailing view around the table (and at the time I reckon, what with curriculum coherence high on agendas) was that it was important to have one clear procedure to dealing with equations, and that a balance method was preferable and that therefore we should take 11 from both sides first and divide by (-2). If we were to overload students with too many methods then this was not good for procedural recall.
I countered that this was ridiculous for an equation such as 10-x=7 and how crazy it would be to insist that students subtracted 10 from each side first.
I rarely teach solving equations as new. Taking on students from Year 10 means that students always come to us with equation methods already, but often they struggle with equations such as these as they are unconventional, and the standard procedures are clunky for them. I teach it with an open box.

Here is a question that all students in my experience (of 14+) could answer.
Yet I have had even potentially high attaining students struggle with the identical:

Viewing x as a window we see:

Because of the window we see the equivalence and it brings that familiarity.
Similarly:

The open box is our window between the world of arithmetic and algebra. It highlights the change between the two worlds. On one side of the window is 2x and on the other side of the window is 8. The conceptual understanding of the window drives this.
Of course, whilst this method could work with other, more complex equations, we need to stop. This is a technique for specialisation – when we are stuck on problems, we specialise (There’s a quote which I’m sure is attributable to John Mason “If you’re stuck, specialise”, but I can’t find a reference to it anywhere, so I’m worried I’ve made it up). This is a technique for helping us out of a hole when we are not sure what to do. We look through the window and use it to help us to see.
The window can also be used to elaborate on different approaches and methods. Take, for example, 3(x + 2) = 24. A while ago I was working on this with year 10 and all their methods were multiplying out brackets and solving, but I wanted them to see alternatives, so I wrote:

The box was the window to this method, and it allowed them to understand the technique more effectively.
Line Equations
Again a reminder here that I teach Year 10+. This was an approach I took with very low prior attaining students, but I have developed this for higher foundation students too and again I think it’s really useful in pulling them away from the procedure and thinking more carefully about the relationships. A real difficulty in this topic is it is easy to teach it in a very algebra focused way, when in fact it is about relationships between numbers.
Last year I approached line equations like this:

I gave the class this image and asked them to write down as many pairs of numbers that they could that went into the boxes.
We then explored how we could turn these pairs of numbers into coordinates:

I push the students to be as creative as possible here, with loads of praise for students who risk using decimals, negatives, fractions or exceptionally large numbers.
Then I plot these coordinates onto graphing software and ask the students to notice stuff. It’s great when they’ve gone for exceptionally large numbers because after they’ve spotted the initial ones all line up, you’re zooming right out and building the tension of finding their coordinates and seeing whether they lie on the line.
Sure I could do all this with y = x + 3, but by using an open box it has less threat, students are better prepared to take risks, because I’m meeting students on this topic where they are at. The boxes are our window between the numerical world and the algebraic world.

A large conceptual leap here is that there are infinite answers here – the windows are open vessels that we could put anything into – but whatever we put in one box influences the other box.
By establishing the window to begin with we later develop the reverse step of being introduced within the algebraic world and looking back through the window towards the number world.

This helps to develop the pairs that we use to establish the relationship. This is fine – modern GCSE questions don’t ask for a table of values to be filled in. Not that I think this technique would struggle with that.
Once the bridge has been built between the numerical and algebraic understanding the algebraic understanding is appropriately scaffolded. There is value in exploring:

or

perhaps, but realistically this is foreshadowing work that should be taught from a basis of good algebraic understanding, that has proper foundations in the simple relationships that I have talked about here.
Ratio
Here is an example of the window moving us forward rather than it being something for looking backwards.
The empty box is something that I have used in my ratio teaching in the past few years. However, viewing it as the window between the worlds of number and algebra develops an opening for higher problem solving with ratio and could scaffold us up to really tricky problems.

If we see the boxes as windows though (and I appreciate this overcomplicates the method for this question, but we use this place where we are comfortable with the method to open up the opportunity later)

3x + 5x = 64
8x = 64
x = 8
3x = 24 and 5x = 40
We can scaffold this up to later problem solving

So initially Alfie has 2x and Benji has 5x. Benji gives Alfie £10 so now Benji has 5x-10 (across 5 parts) and Alfie has 2x + 10 (across 4 parts). So we set up the equation:

There are plenty more questions here on this don steward post, where taking an algebraic approach (built from the window/open box) could have benefits.
I put the Alfie and Benji question on twitter and I think I prefer the ways that avoid algebra, however to show how algebra can sit alongside these approaches I think is important.
As I prepare for Year 7 starting for the first time in my current school, a lot of my job is looking back at what they do in primary schools. In those schools I have been shown their calculation policies which map out the progression in how skills in mathematics should be taught. When I look at ratio problems such as the above, should we move to scaffold that up to algebraic understanding? It is an easy way to represent problems in algebra? Could a secondary calculation policy build up to this to enable multiple tools for problem solving?